Une enquête est seulement valable quand elle est fiable et représentative pour votre business. Il est alors essentiel d’estimer une taille d’échantillon correcte. Cela vous paraît un peu compliqué ? Heureusement ce n’est pas du tout le cas. Vous n’avez que besoin de notre calculateur de taille d’échantillon.
Un entrepreneur qui veut savoir si son produit ou service sera bien reçu, peut lancer une enquête pour explorer le marché. Mais qui interroger ? Et de combien de répondants avez-vous besoin ? Si vous ciblez le marché belge, vous avez un public d’approximativement 11 millions de gens. À combien d’entre eux devez-vous envoyer une enquête pour obtenir une image représentative de votre population ? 1, 5, 10 pour cent de la population totale ? Il ne semble que des hypothèses, mais évidemment ce n’est pas le cas.
Quelle est la taille d’échantillon ?
Deux concepts sont importants pour la représentativité de votre enquête :
- la marge d’erreur : C’est la déviation (positive ou négative) que vous permettez dans les résultats de votre échantillon comparé avec le groupe-cible entier. Si vous calculez une marge d’erreur de 5 pour cent et votre produit paraît sympathique pour 90 pour cent de vos répondants, vous pouvez admettre qu’au moins 85 pour cent et au maximum 95 pour cent de la population belge soit favorable à votre idée.
- le niveau de confiance : Ce pourcentage vous dit dans quelle mesure vous pouvez être sûr de la marge d’erreur. Autrement dit : dans quelle mesure faites-vous confiance dans les réponses données par les répondants ? 95 pour cent est la norme dans le monde d’études de marché.
De combien de répondants avez-vous besoin ?
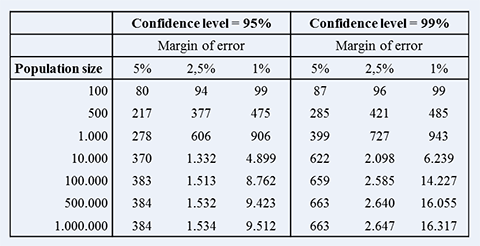
Une fois que vous avez déterminé l’accuratesse des données de votre échantillon, il est temps d’estimer de combien de répondants vous avez besoin (des répondants étant des personnes qui remplissent entièrement votre enquête). C’est possible à l’aide du tableau ci-dessous, mais c’est encore plus simple avec notre calculateur de taille d’échantillon.
Remarquez que les différences sont minimales pour des grandes populations (à partir de 100.000). Pour une étude représentative en Belgique, par exemple, avec une population de 11.000.000 de gens, nous avons besoin de 384 répondants si nous tenons compte d’un niveau de confiance de 95 pour cent et une marge d’erreur de 5 pour cent.
Et le taux de réponse ?
Savez-vous de combien de répondants vous avez besoin pour une étude représentative ? Merveilleux ! Mais tenez en compte que ne pas tout le monde remplira votre enquête – même si elle fait plaisir à voir ! Pour une enquête en ligne, un taux de réponse de 20 pour cent est déjà très bien. Alors, si vous voulez recevoir 400 enquêtes complètes, vous devrez envoyer votre questionnaire à environ 2.000 personnes.
Puis vous voilà prêt à envoyer votre première enquête.
Enregistrez-vous gratuitement !

7 comments
Join the conversationsara - août, 2019
Bonjour, svp pour une population de 140, j’ai reçu 78 réponses (questionnaire auto-administré). Y a-t-il un problème de représentativité? quand-est-ce-que la taille de l’échantillon n’est pas très importante? merci bcp
Gert Van Dessel - septembre, 2019
Bonjour Sara,
La représentativité n’a rien à faire avec la significance de votre échantillon.
Un échantillon peut être statistiquement significatif mais pas représentatif et vice versa.
Avec 78 réponses sur une population de 140 votre marge d’erreur est 7,4% pour un niveau de confiance de 95%.
La représentativité est déterminée par la composition de l’échantillon qui doit être comparable à celle de la population.
Michael R - mai, 2019
Bonjour,
Comment faites-vous pour calculer une marge d’erreur grâce au calculateur sans connaître l’écart type de la population générale ? Est-ce que vous utilisez un écart type standard ou quelque chose de ce type ?
Bien à vous
Gert Van Dessel - juin, 2019
Bonjour Michael,
La marge d’erreur est dérivé des formules suivants:
SS = (Z-score)² * p*(1-p) / (marge d’erreur)² pour des populations infinies
Ajustement pour une population finie:
SSadj = (SS) / 1 + [(SS – 1) / population]
Si la proportion p est unconnue, on prend 0,5.
Pani - septembre, 2018
Bonjour je souhaiterais vous poser une question.
Je suis actuellement en création de société et pour mon étude de marché j’aimerais effectuer un questionnaire dans une ville particulière, cette ville est composée de 1064 personnes.
Si je suis votre calcul j’obtiens :
Taille d’échantillon = ((Seuil de confiance) ² * Proportion (si inconnue mettre 0.5) *(1-Proportion)) / (marge d’erreur) ²
SS= ((1.96) ² * (0.5*(1-0.5))) / (0.05) ²
SS= (3.8416 * 0.25) / 0.0025
SS = 384.16
Ensuite (Votre calcul évoluait en cours de route pour une meilleur compréhension je l’ai modifié à la base sans altérer le résultat)
Taille d’échantillon ajusté = (SS/1) / [((SS – 1) / population totale) + 1]
SSadj = (384.16/1) / [((384.16 – 1) / 1064) + 1]
SSadj = 384.16 / 1.3601128
SSadj = 282.48 … Soit environ 283 pers
Cependant mon étude porte sur le marché de la pizza et je sais grâce aux données d’une étude réalisé par un cabinet spécialisé que 96 % de la population Française aime la pizza, cependant par sureté je souhaiterais prendre non pas 0.96 mais 0.90 en proportion (Soit une marge d’erreur de 6% dans la proportion nationale).
J’obtiendrais pour le coup un calcul de ce type :
SS = (Seuil de confiance) ² * proportion (si inconnue mettre 0.5) *(1-proportion) / (marge d’erreur) ²
SS= ((1.96)² * (0.9*(1-0.9))) / (0.05)²
SS= (3.8416 * 0.09) / 0.0025
SS = 138.2976
Alors
SSadj = (SS/1) / [((SS – 1) / population) + 1]
SSadj = (138.2976/1) / [((138.2976 – 1) / 1064) + 1]
SSadj = 138.2976 / 1.129039097744361
SSadj = 122.49 … Soit environ 123 pers
Pensez-vous que je puisse utiliser cet échantillon significatif de 123 personnes dans mon cas ? Ou dois-je utiliser les 283 pers ?
Je vous remercie de votre retour.
Gert Van Dessel - septembre, 2018
Pani, j’avais déjà répondu votre question il y a quelques jours:
Si votre seule question est ‘Aimez-vous la pizza?’ la 2ième option devrait suffir (donc un échantillon de 123 personnes).
Si vous posez aussi d’autres questions dans votre questionnaire dont vous ne savez pas le résultat d’avance, il faut prendre la première option.